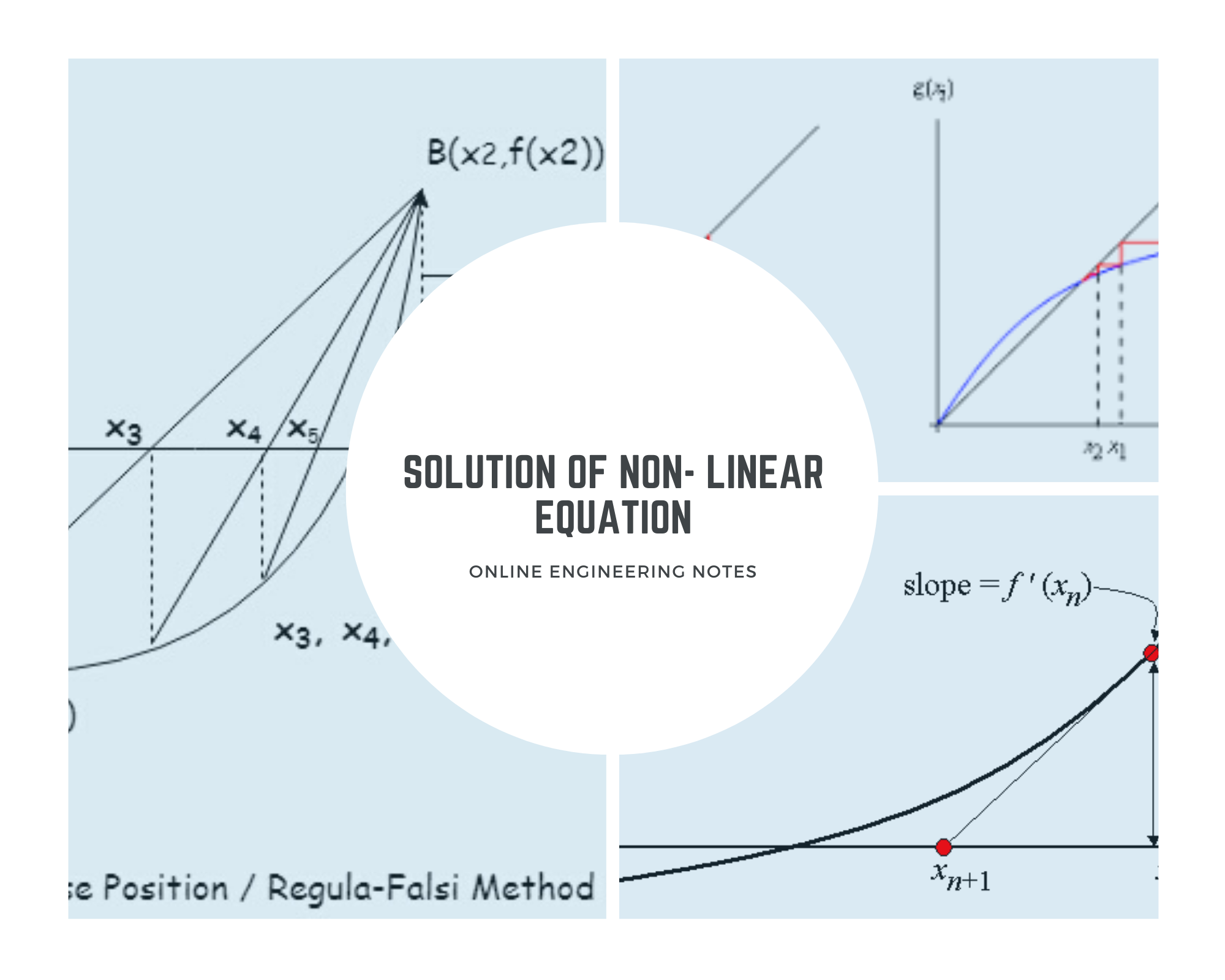
Chapitre III-Numerical Resolution of Non-Linear Equations

One of the most basic problems of numerical approximation, the root-finding problem. This process involves finding a root, or solution, of an equation of the form f(x) = 0, for a given function f . A root of this equation is also called a zero of the function f. The problem of finding an approximation to the root of an equation can be traced back at least to 1700 BCE

ChapII: Numerical Integration

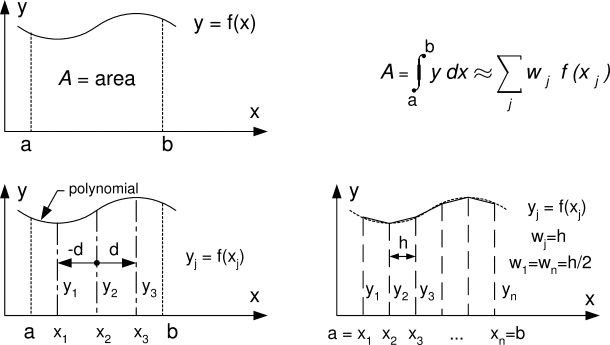
Integration is the process of measuring the area under a function plotted on a graph.  Why would we want to integrate a function?  Throughout many engineering fields, there are (what sometimes seems like) countless applications for integral calculus. 

Sometimes, the evaluation of expressions involving these integrals can become daunting, if not indeterminate.  For this reason, a wide variety of numerical methods has been developed to simplify the integral. 

Here, we will discuss the trapezoidal and Simpson rules of approximating integrals of the form:

\( I= \int_{a}^{b}{f(x)dx} \)